Les amateurs de jeux de cartes savent qu’il faut accorder beaucoup d’attention au brassage des cartes pour éviter la triche, mais qu’en est-il par exemple dans les jeux de poker en ligne ?
Les informaticiens se sont beaucoup cassé la tête sur le tri des données, mais relativement peu sur les problèmes de brassage, moins fréquents et apparemment plus simples. Mais comme disait M. Poisson : « il faut se méfier des appâts rances » ©…
Examinons pour commencer un algorithme tout bête que j’avoue avoir utilisé plusieurs fois : on échange la première carte (ou donnée) avec une autre choisie au hasard parmi les N cartes*, puis on fait de même pour la 2ème carte, la 3ème et ainsi de suite jusqu’à la N-ième. Cette méthode semble réunir toutes les caractéristiques d’un bon algorithme : simplicité, rapidité, et efficacité.
(Si vous avez un vrai browser, voyez cette animation de l’algo. C’est ma première oeuvre faite avec D3.js, fortement inspirée de [1], et que j’essaie désespérément d’inclure directement dans cet article…)
Et pourtant, un tel brassage s’avère « biaisé » : toutes les permutations possibles n’ont pas la même probabilité d’être produites. Déjà en ne brassant que N=3 cartes par cette méthode, 3 des 6 permutations possibles sont nettement moins probables que les 3 autres [3].
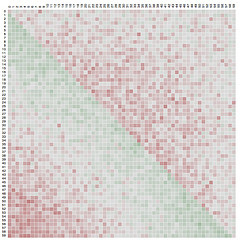
Avec N=60 cartes, ce biais est bien visible sur la figure ci-contre, produite par une autre application D3.js en ligne [2]. Elle effectue 10’000 mélanges avec le même algo, compte dans une matrice le nombre de fois ou la i-ième carte se retrouve à la j-ième position après le brassage, et représente les biais positifs en vert et les négatifs en rouge.
La variante « swap (random ↦ random) » dans laquelle on échange N fois 2 cartes choisies au hasard n’est pas meilleure : elle présente un biais positif sur la diagonale (i=j) qui s’atténue si on effectue 2N échanges, et disparaît presque pour 3N échanges.
Signifierait-ce qu’il faut plus de N opérations pour obtenir un « bon » brassage de N cartes ? On pourrait le penser car il existe un algorithme tout simple sans biais : extraire successivement des cartes prises au hasard dans le tas pour en constituer un deuxième, mais il nécessite N.log(N) opérations***, voire N² s’il est mal programmé [1]. Or N.log(N) est la complexité des algorithmes de tri, donc on pourrait avoir l’idée aussi surprenante que séduisante de se faire un brassage en utilisant quicksort auquel on passe une fonction aléatoire comme critère de tri.
C’est tellement beau que j’exhibe même ici le petit bout de code Javascript qui fait ça:
function shuffle(array) {
array.sort(function() {return Math.random() - .5});
}

random() renvoie un nombre aléatoire entre 0 et 1, donc Math.random() – .5 tire à pile ou face si une carte est « plus grande » que l’autre lors du tri, ce qui est supposé mélanger au lieu de trier.
Cette méthode produit la matrice de biais ci-contre, dont la non-trivialité me laisse pantois.
Par contre, la variante dans laquelle on commence par générer un vecteur de nombres aléatoires, puis on « dé-trie » les données en utilisant ces nombres aléatoires pour les comparaisons donne un résultat non biaisé. (voir « sort (random order) » dans [2])
Et une fois qu’on est tout content d’avoir trouvé un algorithme de brassage non biaisé de complexité N.log(N), on découvre celui de Fisher-Yates datant de 1938, non biaisé, assez simple :
function shuffle(array) {
var j = array.length, t, i;
while (j) {
i = Math.floor(Math.random() * j--);
t = array[j];
array[j] = array[i];
array[i] = t;
}
}
Les 3 dernières lignes échangent les cartes en i-ième et en j-ième position tout comme dans notre premier algorithme naïf, mais ici on ne choisit la carte à échanger que parmi celles qui n’ont pas encore été traitées. Et pour des raisons de simplicité du code, on mélange le tableau « depuis la fin ».
Et le plus beau est que sa complexité algorithmique est proportionnelle à N, ce qui est in exemple de plus de l’universalité du principe de Murphy de la thermodynamique de la tartine beurrée qui dit qu’il est toujours plus facile de générer du désordre que de l’ordre.
D’autre part, si vous devez brasser beaucoup de données de manière irréversible, je ne sais pas moi, pour une application de vote par internet par exemple, souvenez-vous de Fisher-Yates. Et utilisez un vrai générateur de nombres aléatoires , car un générateur de nombres pseudo-aléatoires peut non seulement souffrir de biais, mais surtout être reproductible à partir de la « graine » et permettre ainsi d’inverser le brassage.
Bon, je voulais encore modéliser différentes techniques de brassage de vraies cartes en JavaScript pour déterminer combien d’opérations sont nécessaires pour obtenir un mélange sans biais, mais je préfère laisser ça en exercice pour ChipRaptor et d’autres.
Notes:
Gag © Pierre-Alain de WPanorama
* et non N-1, car il faut garder une chance sur N que la carte soit « échangée avec elle même » et reste à sa place dans le tas.
** félicitations au premier lecteur qui calculera les probabilités respectives de ces permutations et expliquera ainsi le biais…
*** parce qu’on doit alors forcément parcourir des listes ou tableaux
Références:
- Mike Bostock, « Fisher–Yates Shuffle« , 14 janvier 2012
- Mike Bostock, « Will it shuffle ?« , 21 janvier 2012
- Jeff Atwood « The danger of naïveté« , 2007, Coding Horror





4 commentaires sur “Comment bien brasser les cartes”
Excellent la librairie ! Pas possible d’intégrer l’animation sur un site extérieur ?
Normalement c’est du pur JavaScript+CSS, donc intégrable n’importe où, mais les CMS à la WordPress gèrent plutôt JS et surtout CSS dans le « thème » que dans le contenu. D’autre part les browsers (IE…) ne gèrent pas tous le HTML5 utilisé par d3js. Et il y a des questions de sécurité aussi…
J’ai essayé d’inclure le JS nécessaire avec le plugin http://www.nutt.net/2012/06/21/plugins-for-inserting-js-and-css-into-posts/ mais sans succès.
Bref, la techno n’est pas encore vraiment mure. Mais ça viendra
Ha oui c’est un peu mon problème aussi avec WordPress. J’ai utilisé un peu de php dans mon dernier post mais javascript jamais essayé.
Et sinon dans le même genre de librairie javascript pour la visualisation de données (streaming cette fois) j’ai découvert récemment visual sedimentation http://www.visualsedimentation.org/index.html
Wow joli la visualsedimentation ! Et plus encore la http://code.google.com/p/box2dweb/ ! Box2D étant le moteur des Angry Birds, je sens que je vais causer de ça un de ces jours 🙂