Warning: Undefined property: stdClass::$subjects in /home/clients/35666af5317ba4b26577e5dc7df1a2a0/web/wp-content/plugins/openbook-book-data/openbook.php on line 222

Les nombres premiers ont beau être étudiés depuis au moins 2300 ans, ils n’ont jamais été aussi mystérieux ni utiles qu’aujourd’hui.
Mystérieux, car la démonstration de l'hypothèse de Riemann, qui permettrait de définir la répartition des nombres premiers, attend toujours son futur millionnaire.
Utiles, car nos cartes à puces, téléphones et ordinateurs consomment des quantités industrielles de « grands » nombres premiers, en particulier pour le cryptage RSA. La sécurité de cette méthode « asymétrique » repose sur le fait que la factorisation entière en nombres premiers de grands nombres demande un temps prohibitivement long, alors qu’il est très rapide de trouver de grands nombres premiers.
Comment trouver de petits nombres premiers
Ceci parait surprenant de prime abord, puisqu’on apprend à l’école à déterminer si n est premier en tentant de le diviser par les nombres premiers déjà connus inférieurs à √n, ce qui n’est autre qu’une factorisation. On découvre à l’école aussi le crible d’Eratosthène, qui fournit depuis 2000 ans les nombres premiers les uns après les autres à tous les heureux possesseurs de feuilles quadrillées ou de mémoires informatiques:

Cette méthode n’a été légèrement améliorée qu’en 1999 avec le crible d’Atkin et reste excellente pour créer des listes de nombres premiers consécutifs. Ainsi le site www.bigprimes.net les fournit tous jusqu’à 32 416 187 567 *
Mais alors, comment le célèbre Pierre de Fermat a-t-il pu répondre en 1643 à un certain Marin Mersenne (dont nous reparlerons plus bas):
Vous me demandez si le nombre 100 895 598 169 est premier ou non, et une méthode pour découvrir, dans l’espace d’un jour, s’il est premier ou composé. À cette question, je réponds que ce nombre est composé et se fait du produit de ces deux : 898423 et 112303, qui sont premiers.
Et bien parce que 3 ans plus tôt il avait pondu et démontré lui-même son »petit » théorème, qui constitue en même temps le premier test de primalité probabiliste. Grâce à cela, il a su « rapidement » que 100895598169 n’est pas premier. Par contre, comment il a effectué les opérations et factorisé le nombre avec un papier et un crayon en un seul jour, ça je n’en ai avais aucune idée **
Et je ne sais pas non plus comment Mersenne a généré 898423 et 112303 parce que bizarrement, ce ne sont pas des nombres de Mersenne, dont nous parlerons plus bas… En fait, ô surprise, 898423 = 112303 x 23-1, donc Mersenne a généré le grand premier à partir du petit, lequel a d’ailleurs la même forme : 112303 = 7019 x 24-1.
Comment trouver de très grands nombres premiers
Il existe donc des méthodes pour générer des nombres premiers. Aucune ne produit des nombres premiers « à tous les coups » ( ce serait le Graal que certains recherchent encore mais qui n’existe probablement pas ), mais ces méthodes fournissent des grands nombres qui ont une probabilité d’être premiers nettement plus élevée que des nombres de même taille choisis au hasard.
Au IXème siècle déjà, Thābit ibn Qurra avait remarqué que pas mal de petits nombres premiers ont la forme « 321 » p = 3×2n-1 . Les nombres de Thebit sont listés dans A002235. Le plus grand connu actuellement est 3×24235414−1 mais aussi 3×27033641+1 qui n’est pas strictement un Thabit à cause du +1 au lieu du -1 final.
Les nombres de Mersenne ont une forme encore plus simple : p = 2n-1 où n est premier. Et Mersenne ne les a pas découverts : Euclide connaissait déjà les plus petits ( 3, 7, 31 et 127 ) en 300 avant J.C. Mersenne en a juste fait une liste en ajoutant 8191 découvert par Ibn Fallus au XIIIème siècle et 131071 et 524287 découverts par Pietro Cataldi en 1588. Et puis il s’est planté magistralement : sa liste incluait les nombres 267-1 et 2257-1 qui ne sont pas premiers et omettait 231-1, 261-1, 289-1 et 2107-1 qui le sont. C’est dommage, car Mersenne n’a ainsi jamais détenu le record du plus grand nombre premier qui a presque toujours été un nombre de Mersenne. Depuis 2009, le record est 243112609-1 , qui compte 12 837 064 chiffres, trouvé grâce au programme GIMPS. Le rôle de ce logiciel est surtout de faire passer le génial test de primalité de Lucas-Lehmer qui est déterministe (non probabiliste) mais ne marche qu’avec les Mersenne.
Bref, aucun nombre de Mersenne n’est de Mersenne et si je n’avais pas autant de lecteurs en République Française, je proposerais de les rebaptiser « repunits premiers » pour souligner leur beauté en binaire. En effet, 2n-1 s’écrit simplement avec une suite de n « 1 » en binaire. Par exemple 127= 27-1 s’écrit 1111111 en binaire.
Il existe plusieurs autres formules fournissant des candidats premiers :
- Les nombres de Fermat de la forme 22n + 1. Fermat pensait qu’ils étaient tous premiers, mais c’est faux : seuls les 5 premiers le sont, les 28 suivants ne le sont pas, et les autres sont trop grands pour être testés.
- Les premiers de Proth sont de la forme k·2n+1 ( A080075 , record 659×2617815+1 )
- Ceux de Woodall : n·2n--1 ( A003261, 3752948 × 23752948 − 1)
- Ceux de Cullen : n·2n+1 ( A005849, 6679881 · 26679881 + 1)
- les « Cullen généralisés » : n·bn+1,où n+2 > b ( record 427194 × 113427194 + 1)
on voit qu’elles sont toutes des généralisations ou cas particuliers des autres, et que les repunits y jouent un rôle important. Les nombres premiers de Sophie Germain (PSG) sont des nombres p tels que 2p+1 est aussi premier (A005384). Ce « générateur » fournit des nombres moins grands que les autres, mais soulève plein de questions intéressantes : quelle est la longueur maximale d’une chaîne de Cunningham formée par des PSG, y’a-t-il une infinité de PSG etc. Et de plus, le théorème de Sophie Germain établit un lien entre le « petit » théorème de Fermat susmentionné et le grand qui a obsédé les matheux jusqu’en 1994. Et comme je n’ai pas compris grand chose à sa démonstration, je suis plein d’admiration pour cette dame autodidacte qui étonna les mâlethématiciens d’il y a 200 ans.
Si vous voulez vous aussi devenir célèbre, mais facilement, participez à PrimeGrid, une application de la plateforme de calcul distribuée BOINC qui chasse les records de grands nombres premiers. Avec un peu de chance le prochain grand nombre premier sera découvert sur votre ordinateur tout en vous chauffant pous la science.
Comment trouver des nombres premiers d’une longueur donnée
Fin 2009, une équipe internationale a cracké un code RSA-768, en factorisant le produit de deux nombres premiers de 120 chiffres à l’aide de l'algorithme de factorisation par crible sur les corps de nombres et de beaucoup d’ordinateurs. Cet exploit signifie qu’une clé RSA nécessite aujourd’hui des nombres premiers d’au moins 512 bits, soit 154 chiffres décimaux pour être indécryptable.
Nous avons vu plus haut comment obtenir tous les nombres premiers nettement plus courts, ou quelques nombres premiers nettement plus longs, mais pour RSA, nous avons besoin d’obtenir en quelques secondes des nombres premiers de 154 chiffres, avec un seul petit processeur enfermé dans le boitier d’un routeur par exemple, et sans que le nombre transite par un réseau où il pourrait être intercepté. De plus, le nombre ne doit pas être stocké dans une table dont un pirate pourrait essayer les combinaisons : il doit être généré aléatoirement.
Mais au fait, existe-t-il beaucoup de nombres premiers de 154 chiffres ? Oh que oui : la densité des nombres premiers autour de n est de 1/ln(n), or 1/ln(10154) donne environ 0.3% : environ 3 nombres de 154 chiffres sur 1000 sont premiers, donc il y en a des giga milliards de floppées. Donc tout ce que notre petit routeur a à faire de temps en temps c’est:
- générer un nombre aléatoire de 154 chiffres en tirant au hasard 511 bits à pile ou face, et en ajoutant un 512ème bit = 1 pour faire un nombre impair. facile et ultra rapide.
- vérifier si le nombre est premier à l’aide d’un test de primalité probabiliste plus moderne que celui de Fermat comme celui de Miller-Rabin.
- si le test dit que le nombre n’est pas premier, ajouter 2 au nombre aléatoire pour obtenir le nombre impair suivant et recommencer l’opération 2. Il faudra répéter ceci en moyenne 300 fois avant que Miller et Rabin disent « probablement premier »
Pour vous faire une idée de la vitesse de ceci, allez au milieu de cette page et cliquez le bouton « auto generate prime number p and q » : vous obtiendrez 2 nombres premier de 512 bits pour le prix d’un seul click.
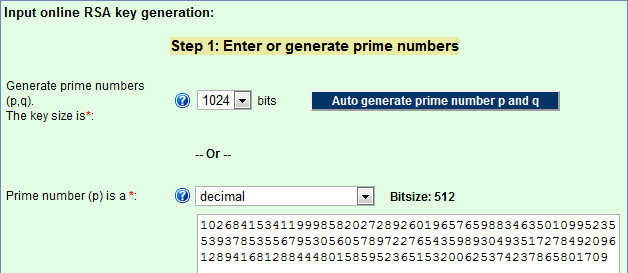
Oui mais, me direz vous, les tests probabilistes ne garantissent pas absolument que les nombres soient premiers. Il y a un risque qu’on encode le message avec une clé foireuse, et donc qu’il soit « facile » à décoder.
Effectivement, mais on admet généralement que la probabilité qu’un nombre de cette taille soit pseudopremier est de l’ordre d’une sur 1030. Et si votre message est si précieux que vous n’êtes pas prêt à courir ce risque, réfléchissez à ceci : le risque qu’un rayon cosmique change un bit du nombre pendant un test de primalité déterministe est un million de fois plus élevé ! J’aime bien cette idée qu’un algorithme probabiliste soit plus fiable qu’une machine considérée comme déterministe, pas vous ?
Notes :
* 32’416’187’567 est tellement proche de 8*2^32 que j’ai une petite idée de la mémoire utilisée par le crible…
** ajout du 18 mai 2014 : Blogdemaths a éclairé ma lanterne à ce sujet dans un article intitulé « Savez vous factoriser à la mode de Fermat ? »
Pour en savoir plus
- L’algorithme RSA sur le Site du Zéro
- Jean-Paul Delahaye "Merveilleux nombres premiers" (2000) Pour la Science ISBN:9782842450175 WorldCat Goodreads Google Books
- nzmath.prime : une librairie Python avec les fonctions qu’il faut





35 commentaires sur “Comment trouver des nombres premiers”
Dr GOULU
Nous avons proposé une nouvelle théorie qui permet d’obtenir, entre autre chose, un générateur de nombres premiers: http://mathscience.tsoftemail.fr
Qu’en pensez-vous ?
merci
Je suis impressionné. Vous avez fourni un travail très important et avez pris la peine de le mettre en forme dans des documents très lisibles (mais volumineux, je n’ai pas tout lu…). Il me semble que vous avez mis le doigt sur quelques recettes qui pourraient en effet être utiles en pratique, par exemple le fait de pouvoir utiliser le test de Lucas-Lehmer plutôt qu’un test probabiliste.
Cela dit, n’étant pas un mathématicien spécialiste de la théorie des nombres je ne peux pas me prononcer sur la valeur de vos résultats sur le plan strictement scientifique, mais quelques imprécisions me font penser qu’il faudra un travail de formalisation et de démonstration conséquent pour pouvoir utiliser vos résultats.
Par exemple dans le document de synthèse vous dites:
« Entre deux nombres impairs consécutifs au carré comme par exemple [37^2 , 39^2[ , aucun des nombres composés dans cette intervalle ne peut être un multiple d’un
nombre premier supérieur à la borne inférieur de cet intervalle, soit dans cet exemple 37 »
or entre 1369 et 1521 il y a:
1371=3*457
1379=7*197
1383=3*461
1385=5*277
1387=19*73
1389=3*463
1391=13*107
1393=7*199
1397=11*127
1401=3*467
1403=23*61
1405=5*281
1411=17*83
1415=5*283
1417=13*109
1437=3*479
1441=11*131
1457=31*47
1461=3*487
1465=5*293
1469=13*113
1473=3*491
1477=7*211
1497=3*499
1501=19*79
1507=11*137
1509=3*503
1513=17*89
1517=37*41
qui sont tous divisibles par des premiers > 37 (je me suis limité aux impairs qui n’ont que deux facteurs, sinon il y en aurait encore plus…)
Il est possible que j’aie mal compris ce que vous vouliez dire, mais ce que je veux dire est qu’une construction mathématique est quelque chose d’extrêmement rigoureux où un certain formalisme est hélas indispensable pour réduire à quasi néant les erreurs, fussent-elles d’interprétation.
Bonjour,
vous avez parfaitement raison sur la rigueur nécessaire pour réaliser une démonstration mathématique.
C’est un exercice très difficile auquel personne ne peut prétendre ne jamais faire d’erreur.
C’est pour cela que le travail doit être soumis à validation. C’est en cours.
Concernant votre remarque, il se trouve que je me suis mal exprimé dans ma synthèse car ce n’est qu’une synthèse et l’on ne peut pas mettre tous les détails. En examinant en détail le chapitre I traitant ce sujet, vous auriez compris que ce que je voulais dire est que, en reprenant votre exemple, tous les nombres composés impairs entre 37^2 et 39^2 sont obligatoirement des multiples des nombres premiers compris entre 3 et 37 (37 compris). Il n’y a rien de nouveau dans ce résultat car ce sont les nombres premiers entre zéro et la racine carrée d’un nombre impair compris entre [37^2 et 39^2[.
Ce résultat aide à comprendre un élément fondamental que je définis qui est le motif combiné. Cela va permettre de comprendre pourquoi la distance maximale entre deux nombres premiers est liée à l’apparition de nombres premiers jumeaux ! Nous proposons ainsi une démonstration de la conjecture de Legendre. Encore une fois, ce n’est qu’une proposition qui reste à être validée ou pas.
Un résultat intéressant est le théorème que nous proposons pour caractériser tous les nombres premiers sauf les nombres 2 et 3. Ce résultat permet de résoudre des équations faisant intervenir deux nombres premiers. Nous résolvons ainsi l’équation des nombres premiers jumeaux et l’équation de Goldbach. Attention, la résolution de ces équations ne permet pas de résoudre les conjectures associées. Qu’en pensez-vous ?
Le paramètre important à comprendre est que avons une relation entre la valeur d’un nombre et sa racine carrée.C’est le paramètre « j » qui fait la relation. On réduit ainsi la problématique à une seule variable. On retrouve ce paramètre dans toutes nos formules. De plus, on explique également la relation des nombres premiers avec les nombres complexe grâce aux fonctions sinusoïdales associées aux nombres impairs. En fait, on peut traiter le problème des nombres impairs comme un problème de physique ondulatoire. Cela fait donc le lien entre les nombres premiers et PI et l’exponentiel avec la formule de De Moivre. Cela permet également d’expliquer le caractère oscillatoire des mesures observées dans les propriétés des nombres premiers, la spirale d’ULAM…etc.
J’ai mis au point un logiciel de calcul des nombres premiers Gypse.
Dans les petits nombres il peux calculer 120 np par seconde, soit environ 8 000 np par minutes. Pour les np de 7 chiffres 20 np par seconde. Il fonctionne sans interruption, je l’ai testé sur 5 minutes pour l’instant.
Bien 🙂 Il fonctionne sur le principe du crible ou d’un test de primalité ? Est-il disponible quelque part ? Et pourquoi « Gypse » ?
Monsieur,
J’ai l’honneur de recevoir votre réponse. J’ai réalisé ce logiciel Gypse supposé calcul égyptien avec l’aide d’un informaticien. Il n’est pas actuellement sur le marché. Merci Paul Lamour.
Paul.lamour3@wanadoo.fr
Merci pour ces informations Paul mais je suis un peu déçu. Si vous ne donnez ni la méthode, ni le programme, c’est difficile de voir en quoi votre programme apporte un avantage par rapport à ceux qui existent déjà.
Pour information, un simple programme de crible d’Atkin en Python (langage pas particulièrement rapide) fournit les 168 nombres premiers inférieurs à 1000 en 46 millisecondes, selon http://stackoverflow.com/questions/2068372/fastest-way-to-list-all-primes-below-n … Ca fait 3652 nombres premiers par seconde, donc environ 30x plus vite que le vôtre …
Docteur Goulu,
Je sais déjà qu’il y a des logiciels plus rapides. Je teste la longueur des périodes des inverses des nombres premiers et choisis la base de calcul comme 2 ou 10. Le principe est qu’avec un court programme on peut calculer indéfiniment. J’ai testé à partir du nombre 79 pendant 10 minutes et j’ai obtenu 132 pages de 27 271 np soit 45 np par seconde. Dernier nombre à l’arrêt : 2 145 289
Merci Paul Lamour.
Paul.lamour3@wanadoo.fr
Je me permets de préciser que je suis le créateur de cette méthode et que je vais la vendre en CD lors de diverses manifestations. Je souhaiterais donc savoir s’il existe d’autres logiciels qui calculent les np à partir de la période des inverses, afin de prévenir les acheteurs. Merci PL
Ah voilà, ça commence à devenir intéressant (mais ça a été long 😉 ). Vous utilisez le développement décimal périodique de l’inverse d’un nombre premier … Bonne idée mais:
Je pense que c’est pour ces raisons que je n’ai pas trouvé de logiciel générant des nombres premiers ainsi.
Cette approche me semble plutôt ressembler à un test de primalité probabiliste comme le Miller-Rabin dont je parle dans l’article (et qui est extrêmement rapide)
Ce que j’ai trouvé de plus intéressant (en ne cherchant que quelques minutes) c’est cet article http://arxiv.org/abs/1006.4653 qui propose une méthode de cryptage utilisant ces développements périodiques à la place des nombres premiers.
Aujourd’hui les algorithmes sont gratuits et publiés pour qu’on puisse vérifier leur validité. Pour arriver à vendre un logiciel, il faut vraiment qu’il apporte un plus, de la valeur ajoutée pour une application précise.
Docteur goulu,
Je n’ai pas ce logiciel, élaboré par un informaticien, je le lui ai décrit en ancien Basic, et lui ai fourni des variantes Gypsie 2 et 3 et j’espère vendre quelques exemplaires avant qu’il ne circule sur Internet.
Vous pourriez me rendre un deuxième immense service en diffusant ma demande. Il faudrait accepter l’idée d’un club Paul Lamour. En arithmétique je calcule en euclidien pour la multiplication et recherche de diviseurs, et en égyptien pour la recherche de nombres premiers mais ce sont des dénominations sous toute réserve. Je souhaiterais également enseigner mes méthodes de calcul combinatoire et d’autres mal ou pas du tout connues. Merci encore.
Bonjour Paul,
vous devriez fonder votre « club » sous la forme d’un blog comme celui-ci. Je vous conseille vivement https://wordpress.com/ c’est gratuit, facile et très bien référencé (= on trouvera vos pages facilement en cherchant sur Google). Ensuite vous pourrez facilement faire de la pub sur facebook, twitter etc et je relaierai volontiers vos publications.
Pour vendre du logiciel, c’est plus compliqué… Qui sont vos clients potentiels ? Combien sont-ils prêts à payer pour ce logiciel (ou pour chaque utilisation): 1$, 100$, 1000$ ? ça change complètement la manière de le diffuser.
1003517 – 1003397 – 1002917 – 1002797 – 1002787 – 1002517 – 1002467 – 1002427 – 1002347 – 1002227 –
1002077 – 1001947 – 1001797 – 1001587 – 1001387 – 1001267 – 1001237 – 1001197 – 1001027 – 1000907 –
… (DrG : raccourci la liste de 7247 nombres …)
50957 – 50867 – 50627 – 50387 – 50227 – 50147 – 50077 – 49877 – 49787 – 49757 –
49667 – 49547 – 49307 – 49277 – 49157 – 49117 – 49037
La bonne nouvelle, c’est qu’effectivement tous ces 7247 nombres sont premiers.
La moins bonne, c’est qu’il y a beaucoup plus de nombres premiers entre 49037 et 1003517 : il y en a 73729, dix fois plus que vos 7247, ce qu’on peut suspecter quand on voit que tous vos nombres se terminent par 7.
Un bête petit programme Python a trouvé les 73729 en environ 5 secondes, pour info (en utilisant le test de Miller-Rabin)
Maintenant dites moi :
743808006803554439230129854961492699151386107534013432918073439524138264842370630061369715394739134090922937332590384720397133335969549256322620979036686633213903952966175107096769180017646161851573147596390153 est-il premier ?
et quel est le nombre premier juste supérieur ?
Toujours le même test de Miller-Rabin en Python répond aux 2 questions en 0.6 secondes…
Loin de moi l’idée de vous décourager, mais comme j’ai essayé de le montrer dans l’article, il existe des algorithmes vraiment très puissants (=rapides) pour tester et générer les grands nombres premiers dont l’industrie a besoin. L’intérêt d’une nouvelle méthode générant les petits nombres premiers me semble très très limité, à part pour la beauté des mathématiques.
Docteur Goulu,
Merci de tout cœur pour votre nouvelle réponse.
Je n’ai pas créé actuellement de logiciel permettant de répondre à votre question. J’ai mis des années à trouver un informaticien et s’il accepte de continuer je vais passer à une « calculatrice sans fin » qui fonctionne très bien.
Vous pouvez me trouver sur les sites
http://www.plumesdazur.fr/
http://acdcedit.pagesperso-orange.fr/chpm.htm
Actuellement je peux montrer à un élève comment effectuer la multiplication à la main sans calculatrice :
761 009 x 623 474 = 474 469 325 266
Paul Lamour
Bonjour Dr. Goulu,
Vous demandiez comment Fermat a factorisé le nombre 100 895 598 169. J’ai justement écrit un article à ce propos et l’explication se trouve ici:
http://blogdemaths.files.wordpress.com/2014/05/factorisation_de_100895598169_par_fermat.pdf
Si vous voulez lire l’article complet (dans lequel j’explique la méthode de factorisation de Fermat, méthode qu’il n’a probablement pas utilisée pour factoriser 100 895 598 169), c’est ici:
http://blogdemaths.wordpress.com/2014/05/18/savez-vous-factoriser-a-la-mode-de-fermat/
Enfin, il semble que le petit théorème de Fermat n’a pas été utilisé pour montrer que 100895598169 est composé, car le nombre de calculs est assez long… et même en admettant que Fermat connaissait la méthode d’exponentiation rapide (modulaire), voici les calculs qu’il aurait dû faire pour montrer que 2^{100895598169} = 21283103109 ≠ 1 mod[100895598169]: http://i.imgur.com/asdLTBv.png
Bon, on peut toujours penser que c’est possible à la main, mais en un jour ça paraît short ! 🙂
Merci beaucoup et bravo pour vos article + pdf + code Python ( http://pastebin.com/CKDq8Ts4 ) expliquant très clairement ces algorithmes.
Je suis toujours épaté par l’ingéniosité des cerveaux humains lorsqu’ils ne pouvaient utiliser que du papier et un crayon en lieu et place d’ordinateur…
Bonjour Dr,
Vous Pithonez pus vite que votre ombre, merci pour cette rapidité. Je me réexplique
Question 1
La question n’est pas « y a t il une infinité de jumeaux » (bravo aux conjectureurs et démontreurs) mais » chaque fois que l’on rencontre un premier il est la somme d’un premier précédent et d’un nombre qui est lui même le produit d’un certain nombre de fois 2 ; pourquoi alors ne s’intéresser qu’aux jumeaux »
Question 2 (la plus intéressante pour ma quête) « les jumeaux ? il y en a plein (variante locale du beaucoup zinzinien)- une infinité – mais jamais entre ce bon quart de premiers finissant par 3 et ce bon quart de premiers finissants par 7 ; Ils sont tous entre des premiers finissant par : gémellité 1 et 3 gémellité 7 et 9 gémellité 9 et 1
A vous.
Bonjour Dr,
J’ai un petit problème de formulation, dans la littérature je rencontre beaucoup d’articles sur les « couples » de nombres premiers, notamment les p +2 ; eux même premiers.
Mais tous les premiers (sans exception) sont de la forme p’ = p +2.n , pourquoi l’insistance dans les revues sur le 2.1 qui n’est d’ailleurs pas parfait (grande affection entre eux des finissant par 1 et 3 car 1+2=3; entre finissant par 7 et 9 entre 9 et le 1 MAIS, une tendance lourde, confinant à l’exclusivité : xénophobie entre finissant par 3 et 7 )
Est ce que ma formulation p’ premier suivant = p premier connu + 2.n est correcte ? est elle écrite autrement pour … un matheux?
Vous avez compris que j’explore toujours la particularité des premiers à se regrouper exhaustivement en 4 familles chacune caractérisée par, selon votre formulation (03-07-2013), « la dernière décimale ».
Bonne journée à vous et le bonjour aux infirmières.
Essayez d’utiliser le jargon au maximum pour plus de clarté : ce ne sont pas des « couples » de nombres premiers mais des http://fr.wikipedia.org/wiki/Nombres_premiers_jumeaux
p’=p+2n dit juste que p’ est le n-ième nombre impair après p. C’est une condition nécessaire (tous les premiers étant impairs) mais absolument pas suffisante pour déterminer si p’ est premier. Le cas n=1 est juste « le plus simple » : existe-t-il une infinité de nombres premiers jumeaux ? C’est la « conjecture des nombres premiers jumeaux », qui n’est toujours pas démontrée malgré un bon siècle de travaux acharnés.
Mais un résultat très récent fait un grand pas en direction de la preuve qu’il existe une infinité de nombres premiers jumeaux http://www.journaldelascience.fr/technologie/articles/conjecture-nombres-premiers-jumeaux-demontree-3070 , et par extension une infinité de nombres premiers séparés par 2n donné.
Je ne suis pas sur d’avoir bien compris votre idée concernant la dernière décimale : le petit programme plus haut montre que 1,3,7,9 sont équiprobables (les écarts sont « statistiquement non significatifs », sauf peut-être pour le « 1 », à vérifier…). Vous pensez que la distribution est différente pour les jumeaux ? C’est possible…. Alors hop un petit programme:
from nzmath.prime generator def twins(): p1=1 for p2 in generator(): if p2-p1==2: yield p1,p2 p1=p2 def decimals_stats(n=100000): decimal=[0]*10 i=0 for p1,p2 in twins(): decimal[p2%10]+=1 i+=1 if i==n:break return decimalqui donne [0, 33143, 0, 33502, 0, 1, 0, 1, 0, 33353] pour les fréquences d’apparition de la dernière décimale du 2ème jumeau. Il semblerait en effet qu’il y ait un déficit de « 1 », un surplus de « 3 », un seul « 7 » donné par les jumeaux (5,7) et un nombre « normal » de « 9 ».
Depuis ma découverte du https://drgoulu.com/2011/04/10/le-fosse-de-sloane/ , je me demande si les nombres premiers ne seraient pas les nombres les plus inintéressants qui soient, d’où leur répartition fantastiquement aléatoire. En fait on s’y intéresse beaucoup, mais leur « propriété » est en fait une NON-propriété : ils n’ont PAS de diviseurs. Ils sont dans les « trous » du crible d’Ératosthène : ce sont donc les autres nombres qui, étant composés, ont des répartitions régulières et autres propriétés intéressantes.
Bonjour Dr,
Intéressant, il ne faut pas désespérer, enfin une régularité, imparfaite il est vrai, les séries doivent « tendre vers » 25 % pour chacun de la bande des 4. Mais pas sûr, « l’excédent » – très relatif il est vrai – de 7 apparaît très vite dans les factorisations* et aussi longtemps que durent les calculs, pleins de premiers finissant par 7 (4 ou 5, parfois plus) peuplent – et exclusivement eux – le peloton de tête des plus grands premiers obtenus, flippant ! Comme si le 2 et le 5 trop tôt ravis à notre affection « perturbaient » les suites.
* factorisations des nombres issus des progressions r=100 vues plus haut.
Enchanté ravi de votre patience et de votre sens pédagogique, je ne ferai retour vers vous que dans quelques jours ou semaines (ici la mer est chaude) car les liens que vous m’avez suggéré donnent du grain à moudre – leçons de formalisation … – et comme les r=100 génèrent des séries comportant 30 % de premiers, et qu’il me faut 4 séries une de 1, une de 3 une de … mais je ne suis pas pressé.
Sincèrement merci encore.
Bonjour Dr,
Je m’étais habitué à l’idée – qui me plaisait bien – du caractère parfaitement aléatoire de la survenance des premiers.
Or il se trouve que si l’on construit une liste du genre n+100
(et de l’autre côté n-100) (mais ça marche avec d’autres choix- moi j’aime bien 82+100 et 82-100 ; les 41,91 et 8 générés sont plus rigolos-).
Apparaît alors une régularité gênante dans l’apparition du premier premier dans la factorisation
Oublions le 2 et le 5, on a :
82 = 2.41
182 = 2.7.13 °
282 = 2.3.47 *
382 = 2.191
482 = 2.241
582 = 2.3.97 * * –> le 3 apparaît dans la factorisation tout les deux espaces
682 = 2.11.31
782 = 2.17.23
882 = 2.3.3.7.7* ° ° –> le 7 » tout les six
etc. le 11 tout les 10
le 13 tout les 12
le 17 tout les 16
J’arrête là, ça fait un joli dessin sur l’ordi.
Cette régularité gênante a telle un sens ? ou plus humblement puisque l’on est dans l’aléatoire où ai je commis une erreur ? votre site ( si ! si !) m’a paru plus didactique que d’autres.
En un mot est ce grave docteur ?
Bonjour Serge,
vous examinez les facteurs premiers d’une suite arithmétique de raison r (=100 dans votre cas, mais ça ne change rien), donc des nombres de la forme xi=n+i.r
Si un nombre xi a un facteur premier f, alors le nombre xi+f = xi+f.r aura aussi le facteur premier f car f est un facteur commun de xi et de f.r : en fait vous avez le 3 tous les 3, 5 tous les 5 etc. (dans votre message, quand on compte la « distance » entre deux nombres il faut faire une soustraction, donc le 7 qui apparaît au 2ème terme et au 9ème correspond en fait à 7 « espaces », pas 6…)
Je vous félicite d’avoir découvert cette régularité par vous-même, mais elle est hélas « évidente » pour un matheux. Il existe des travaux sur les relations entre suites arithmétiques et nombres premiers, mais il faut s’accrocher : http://images.math.cnrs.fr/Nombres-premiers-et-progressions.html
Bienvenue sur ce blog !
Bonjour Dr,
Merci pour la réponse et pour le lien sur les progressions.
Cette régularité a t elle une utilité pratique ? au minimum vérification de résultats ?
Puis je sans abuser poser une autre question : est il correct de dire – ces suites étant infinies – qu’il y a « autant » de nombre premiers finissant par le chiffre 1 que par les chiffres 3,7,9 ?
Je n’ai pas ma vitale sur moi, mais le coeur y est, avec mes remerciements.
J’aurais tendance à dire qu’il y a beaucoup de régularités entre nombres composés (non premiers), mais qu’on en cherche désespérément une concernant les nombres premiers…
Votre question sur la fréquence des dernières décimales est intéressante, d’autant que je n’ai rien trouvé sur le sujet. Et comme je n’ai pas le niveau pour me lancer dans une démonstration, j’ai préféré l’approche expérimentale du petit programme Python suivant:
from nzmath.prime import generator, def decimals_stats(n=100000): decimal=[0]*10 i=0 for p in generator(): decimal[p%10]+=1 i+=1 if i==n:break return decimal print decimals_stats()qui produit:
[0, 24967, 1, 25007, 0, 1, 0, 25015, 0, 25009]
donc à l’exception du 2 et du 5 qui apparaissent une fois chacun, les 1,3,7 et 9 sont très équiprobables dans les 100’000 premiers nombres premiers
Bonjour,
Il y a quelque chose qui me laisse perplexe dans cette course aux très grands nombres premiers. Pour obtenir un très très très grand nombre premier et battre le record actuel, ne suffit-il pas de calculer le produit de tous les premiers nombres premiers que l’on connaît et d’ajouter une unité ?
D’après Euclide, on est sûr qu’un tel nombre est premier. Et il sera plus grand que le nombre de Mersenne 2^57,885,161 − 1.
Je me doute bien que mon raisonnement doit être faux car, sans ça, d’autres y auraient pensé avant moi. Mais je suis curieux que l’on m’aide à trouver par où mon raisonnement pêche.
D’avance merci pour vos explications !
Votre méthode fonctionne si on multiplie tous les nombres consécutifs, mais pas si on en saute. L’exemple trivial qui me vient à l’esprit est 2 x 7 + 1=15 qui n’est pas premier, car j’ai sauté le 3 et le 5.
Mais je suis en train de me dire que votre méthode appliquée aux 1.4 milliard de nombres premiers consécutifs répertoriés dans http://www.bigprimes.net/ pourrait effectivement donner un nombre premier record d’environ 8 milliard de décimales d’après un calcul rapide et pifométrique !!!
Ca y’est, ça va m’empêcher de dormir … :-/
En fait j’aurais du dormir avant de répondre 😉
Le produit de tous les premiers consécutifs connus +1 n’est pas forcément premier!
D’après Euclide, soit il l’est, soit il est factorisable en premiers qui ne sont pas dans le produit.
Comme quoi il ne faut pas trop se fier à l’intuition et bien lire les théorèmes, même vieux de 2300 ans…
J’ai vite fait le petit Python suivant:
from nzmath.prime import primeq, generator, properDivisors n=1 for p in generator(): n=n*p if primeq(n+1): print p,n+1,"Premier" else: print p,n+1,"="," * ".join(map(str,properDivisors(n+1)))qui affiche pour chaque premier p le produit des premiers jusqu’à p (noté p#) +1 avec sa factorisation éventuelle:
La séquence A005234 donne les nombre premiers « primordiaux » p tels que p# + 1 (séquence A018239 ) est premier.
En passant, le lien A005234 mentionne deux conjectures très récentes (2013) concernant le nombre premier suivant p# + 1 en fonction de p, donc ce sujet n’est pas clos…
Donc merci Amaury : nos erreurs nous ont permis de découvrir des choses intéressantes 🙂
Merci Dr. Goulu !
Vos explications sont limpides. Je comprends mieux pourquoi la recherche de très grands nombres premiers s’appuie depuis plusieurs années presque exclusivement sur des nombres de Mersenne.
Merci pour l’expérimentation avec le petit code en Python.
Je vais explorer les liens que vous donnez.
salut j’ai trouvé un autre grand nombre premier (plus grand que 1700milliards et quelc.)
svp.aider moi, quesque je doit faire pour contacter les responsables de prime.
Si vous avez trouvé un nombre un peu plus grand que 1’700’000’000’000 ça n’a aucun intérêt. Si votre nombre à plus de 1’700’000’000’000 de chiffres, là c’est intéressant de savoir comment vous avez fait. Mais vous auriez pu prendre 2 minutes de plus pour chercher sur le site primes et trouver la page http://primes.utm.edu/primes/includes/mail.php avec le nom du responsable en bas de la page…
@Vincent : oui effectivement j’avais pris les records sur une page de la wikipédia un peu vieille. Le hic vient aussi des généralisations : effectivement Riesel étant plus général que Thebit, le cas k=3, b=2 bat le record mentionné sous Thebit.
@Erwann : je me rends compte que mon texte n’est pas assez clair pour les initiés : quand je disais qu’il faut passer en moyenne 300 tests de Miller-Rabin, je ne parlais pas des itérations que vous mentionnez mais du nombre moyen de nombres de 512 bits qu’il faut scanner avant d’en trouver un premier. Effectivement, on peut aussi jouer avec le nombre d’itérations « internes » de Miller-Rabin pour ajuster le risque d’erreur souhaité. Je pense que c’est en partie ce qui explique pourquoi le générateur de la page web soit tellement plus rapide que mon programme Python…
Pour les 1 finaux et terminaux, je ne voulais pas trop rentrer dans les détails, mais merci de le faire pour moi.
Pas besoin de passer 300 fois Miller-Rabin pour un premier de 512 bits. La probabilité qu’un composé passe le test non détecté est de 1/4 à chaque fois.
Pour du RSA, avec 2 premiers de 512 bits, on obtient une clé de 1024 bits, offrant environ 80 bits de sécurité. 40 itérations pour chacun des candidats premiers est donc suffisant. En pratique, on se contente de moins que ça.
Autre remarque, pour obtenir un premier de n bits, on choisit n-2 bits aléatoires, et on « ajoute » 2 bits à 1 de chaque côté. Votre méthode permettrait d’avoir un premier plus petit que souhaité.
bonsoir.
Certains de vos chiffres e sont plus d’actualitée : pour les riesel ( forme k*b^n-1) avec k=3, le plus haut connu est 3 * 2^6090515 – 1
les proth? 19249* 2^13018586 + 1
Si la recherche de record interesse des visiteurs, je vous conseille de faire un tour sur le forum mersenneforum.org (en anglais)