Incroyable : une deuxième tentative d’article scientifique en une semaine dans le torchon du coin café! Ils ont du engager un stagiaire qui vise Science&Vie … Cette fois c’est « Le succès des films tient à une formule de maths. » Attachez vos ceintures :
… les films à succès suivent une formule mathématique. Il s’agit de la « transformée de Fourier ». Derrière ce nom barbare se cache la fluctuation 1/f …
Ouch! Ca fait mal à ceux qui ont étudié le barbare sous toutes ses coutures…
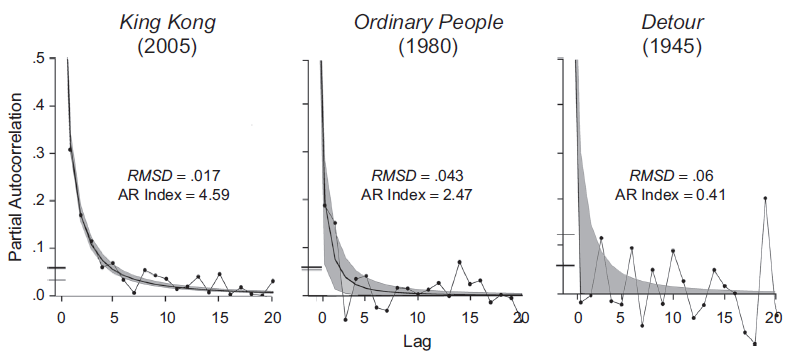
Décryptons. Parce qu’à la base il y a une info, une vraie, qui aurait pu être intéressante si elle n’avait pas été massacrée. James E. Cutting, professeur de psychologie à Cornell a mesuré la durée des plans de 150 films tournés entre 1935 et 2005 [1]. Première chose étonnante : ces films d’une durée moyenne de 126 minutes contiennent de 231 plans pour « Seven Year Itch » (1950) à 3099 pour « King Kong » (2005) , et en moyenne 1132 plans d’une durée toujours aussi moyenne de 6.68 secondes seulement !
L’étude analyse ensuite l'autocorrélation de la durée des plans de chaque film, qui a permis de montrer que « les films hollywoodiens sont devenus progressivement découpés en paquets de plans de durée similaire. Par exemple, les scènes d’action sont typiquement formées de plans relativement courts, alors que les scènes de dialogue sont formées de plans plus longs alternant d’un acteur à l’autre. De ce point de vue, les éditeurs de films ont progressivement augmenté pendant 70 ans leur contrôle sur le mouvement visuel de leurs narrateurs, rendant les relations entre la durée des plans plus cohérente » (traduction personnelle d’un passage de l’article)
Et le barbare là dedans ? La transformée de Fourier permet de décomposer un signal quelconque en une somme de signaux tout simples : des sinusoïdales de fréquences distinctes. Elle permet donc de discerner des périodicités dans des signaux compliqués et bruités. Et de les filtrer. Et de les transmettre. Et de les stocker. Et de les visualiser. Et… Je m’avance peut-être un peu, mais je dirais que Joseph Fourier est l’Archimède des ingénieurs : sans son coup de génie, tous les bidules électroniques fonctionneraient aussi bien que des bateaux en silex massif. Voilà pour le barbare.
Mais pour terminer cet article, il nous faut encore un ostrogoth et un hussard : le théorème de Wiener–Khintchine a dit à Cutting et son équipe qu’en appliquant la transformée de Fourier à l’autocorrélation de la durée des plans déterminée plus haut, il obtiendront la densité spectrale de puissance de chaque film. Ca donne en quelque sorte une mesure de la fréquence de la variation de la durée des scènes (c’est un peu difficile à exprimer avec des mots, en fait… des propositions ?)
Toujours est-il que Cutting montre dans son article que cette densité spectrale de puissance change avec le temps. Il l’approxime par une distribution en 1/fα Au débuts du cinéma, la durée des scènes était proche d’un « bruit blanc » (α=0) comme si la durée d’un plan n’avait absolument aucune relation avec le reste du film. Aujourd’hui, elle s’approche d’une distribution en 1/f (α=1) typique du « bruit rose ».
Là où ça devient vraiment intéressant, c’est que les processus aléatoires qui ont une distribution en 1/f captent apparemment mieux notre attention [4]. Cette distribution est typique des processus complexes, biologiques entre autres : ils sont aléatoires, mais leurs composantes « lentes » sont plus importantes que les « rapides » : ça nous intrigue beaucoup plus qu’un phénomène totalement imprévisible, ou totalement prévisible.
Dans l’article, Cutting doute que les réalisateurs hollywoodiens soient réellement conscients de ceci et que leurs monteurs découpent volontairement leurs plans selon une loi en 1/f. Et si c’était plutôt un processus évolutionniste ?
Bon, ok, à la décharge du journaliste stagiaire, il faut du temps bon marché de blogueur initié et plus de place que quelques lignes pour expliquer tout ça. Et s’il n’avait pas raconté n’importe quoi sur Fourier, je ne me serais jamais intéressé à l’article scientifique sous-jascent, que je trouve excellent. Donc finalement il a fait son boulot…
Références
- [altmetric pmid= »20424081″ float= »right »]Cutting JE, DeLong JE, & Nothelfer CE (2010). Attention and the evolution of Hollywood film. Psychological science, 21 (3), 432-9 PMID: 20424081 [pdf]
- Christine Nothelfer, « Research Bulletin: Making the Cut » 2009, OnFiction
- « Solved: The mathematics of the Hollywood blockbuster« , New Scientist, 28 février 2010
- [altmetric pmid= »11212631″ float= »right »] Gilden, D.L. (2001). « Cognitive emission of 1/f noise ». Psychological Review, 108, 33–56. (pdf)
4 commentaires sur “Succès hollywoodiens et transformée de Fourier”
Très chouette explication. nécessaire vu la citation compacte et fausse de l’article d’origine. L’étude nous apprend que nous prenons intérêt à un spectacle où la répartition d’imprévu et d’attentisme ressemble à l’affût du chasseur ou du pêcheur devant sa ligne, est-ce si étonnant après des centaines de milliers d’années passées à chasser ? Notre capacité narrative elle-même vient certainement aussi de la transmission à autrui de cette expérience mêlant patience et d’action brusque.
Je ne m’y connais pas en signal ni n’utilise régulièrement ces calculs le matin en mangeant mes céréales.
J’aurais l’air d’un vrai Troll simplement en osant commenter le travail du professeur Cutting mais je me lance: quelqu’un aurait-il noter que l’augmentation du nombre de plans en cinéma date de l’avènement de l’évolution au montage numérique du cinéma? Si vous aviez su comment on monte un film en coupant la pellicule à la main, vous auriez vous aussi fait un film avec 500 plans et non 2000. On ne coupe plus les plans de la même manière grâce à la technologie. Le premier King Kong ne pouvait pas être autrement et le dernier King Kong non plus.
Le montage cinématographique a évolué pcq on a su manipuler plus facilement les petits plans par l’arrivée de la vidéo dans un premier temps et ensuite par la numérisation de la pellicule en fichier numérique en un deuxième temps. Les systèmes de montage numérique, s’ils avaient été disponibles pour Cecil B. DeMille, aurait pu l’aider faire ces Dix Commandements aussi excitant que Die Hard, je crois.
Il est amusant de voir une transformée de Fourier varier entre 1955 et 2005 mais je cela aurait pu être aussi intéressant que l’évolution volumétrique du Popcorn collé au plancher des salles entre 1955 et 2005 et y voir une corrélation en fonction du style de film. On sait que les films d’action attirent les jeunes, et que cette clientèle raffole du Popcorn et en échappe plus que le dandy qui va voir un film d’auteur sans rien consommer…
Somme toute, il est quand même utile que vous nous parliez de ce sujet comme prétexte pour causer mathématique.Je crois que votre billet avait sa place pour me faire découvrir de nouveaux théorèmes à moi, le barbare. C’est l’étude de M.Cutting que je tenais à souligner qu’elle pourrait être nominée à un IG Nobels.
Bon,la je deviens un peu mesquin, car M. Cutting n’a quand même pas totalement perdu son temps. Il nous a permis de voir en chiffre cette évolution dans le style de montage hollywoodien des films d’action.
Le Troll que je suis retourne dans sa caverne…
le passage « General Discussion » au bas de la page 6 de l’article aborde certaines de vos interrogations. Il y est montré que l’évolution est beaucoup plus continue que ce qu’on pourrait supposer. Il n’y a apparemment pas eu de Révolution du montage numérique.
Oui, faire du traitement du signal sur les scènes de cinéma pourrait mériter une nomination aux IG Nobel, mais je suis sur qu’on peut trouver encore plus absurde …
Waouh. Je n’y connais rien en traitement du signal mais j’ai à peu près compris. Quel pédagogue !