Pour gagner un match de tennis, il faut gagner des « sets ». Et pour gagner un « set », il faut gagner deux « jeux » de plus que son adversaire, et pour gagner un « jeu », il faut réussir deux balles de plus que son adversaire. Quel est l’effet de cette étrange manière de compter les points? Que se passerait-il si on comptait simplement les balles gagnantes de chaque joueur, en terminant un match par un score de 88 à 82 par exemple ?
Il y a quelques années, un article par dans « Pour la Science » [1] montrait que le comptage des points au tennis introduit un effet non-linéaire dans la relation entre :
- la probabilité de gagner une balle
- et la probabilité de gagner un match.
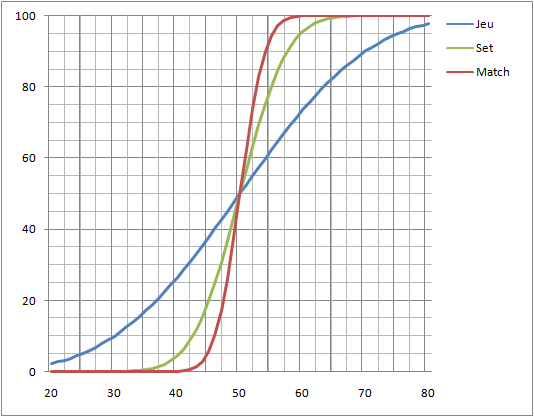
Ceci apparait de façon limpide dans le graphique ci-dessous:
probabilités de gain d’un jeu, d’un set ou d’un match en fonction de la probabilité de gain d’une balle.
J’ai réalisé ce graphique en programmant la simulation de 100’000 matches de tennis entre un joueur gagnant 20% des balles contre son adversaire (qui en gagne donc 80%), puis 100’000 matches lorsqu’il gagne 21% des balles et ainsi de suite. Le programme compte par la même occasion le pourcentage de sets et de jeux gagnés.
Comme on le voit, si en échangeant quelques balles avec Federer vous remarquez qu’il vous laisse en gagner 1/3 (ou que vous êtes vraiment bon), vous n’avez que 10% de chances de gagner un jeu contre lui, mais strictement aucune de gagner un set. Pour avoir 10% de chances de gagner un set contre ‘Rodjeur’, il vous faut être capable de gagner 43% des balles contre lui. Et pour avoir 10% de chances de remporter un match contre lui, il vous faut 47% de balles gagnantes…
Le système de comptage des points au tennis amplifie donc les écarts entre les joueurs : un joueur qui gagne 51% des points contre un adversaire gagnera 62% des matches contre lui. A 52% contre 48%, il gagnera 3 matches sur 4.
Lors du dernier match de Federer contre Stepanek à Rome, le Suisse a marqué 88 pts contre 82 pts à Stépanek, ce qui lui donnait 70% de chances de victoire, mais il a perdu. Stepanek a gagné, malgré moins de balles victorieuses! C’est le prix à payer de la non-linéarité : le comptage des points fait que certaines balles sont plus importantes que d’autres, et donc que celui qui les marque peut gagner avec moins de balles.
Si on gagnait au tennis en étant le premier à marquer, disons 90 points, Federer aurait gagné ce match, mais il en aurait statistiquement perdu beaucoup ces dernières années contre des joueurs qui ne perdent que 1 ou 2% de balles contre lui.
Le système de comptage des points au tennis favorise donc l’apparition de « Numéros 1 » et leur maintien en haut du classement. Tout le contraire du football donc.
Référence :
- L’algèbre du tennis – Pour la science n°127, mai 1988





14 commentaires sur “Le comptage des points au tennis”
A combien de points se termine un match de tennis ?
Wow ! El Jj a fait le même travail par calcul plutôt que par simulation ! Et en plus il a retrouvé la référence que j’avais perdu : L’algèbre du tennis – Pour la science n°127, mai 1988
ça a l’air plus difficile que prévu ??
P.S. : je comprends rien au (e^-Wi+e^WO) etc… c’est quoi e ^- ??
Wow comme vous dites..
Le W5 de Federer en Suisse est de 17.394 et sa valeur de compétition C est de 18.351 et il est évidemment No 1 suisse.
Moi j’ai 11 ans et demi et je suis 14’000ème environ suisse et mon W5 est 0.892 et ma valeur de compétition C est de 1’480 (enfin je devrais dire était puisque se sont des chiffres qui datent de mars 2008. J’étais classé R8 et je serai R7 en octobre avec les nouveaux classement semestriels).
Donc le calcul ne pourrait être qu’approximatif puisque tournoi après tournoi ces valeurs automatiquement changent en fonction si on a gagné ou perdu des matchs je suppose.
Merci d’aider les joueurs de tennis à compter ces maudits points.
wow ! ça c’est du règlement sportif avec des formules et tout 😉
après une rapide lecture en diagonale, il me semble que ce n’est pas directement le classement de votre adversaire qui compte mais sa valeur de compétition « Wi » par rapport à la votre « W0 ». Supposons pour simplifier que vous l’affrontez dans un tournoi ou il n’y a qu’un seul match, entre vous deux.
Si vous gagnez, votre nouveau W vaut ln(e^Wi+e^W0)/2 et si vous perdez c’est W=-ln(e^-Wi+e^-W0)/2
En fait le calcul se fait sur tous vos matches joués sur une année, si j’ai bien compris.
J’ai rien pigé à l’histoire des 5 procédures de calcul et à la « prime de risque » (la formule de l’art 7 est foireuse, en plus). Je vais relire tout ça tranquillement et peut-être pondre un article car je ne pensais pas qu’on puisse pondre un règlement sportif si touffu 😉
Connaissez-vous votre « W » ? et celui de Federer ?
je vous ai envoyé un mail pour le calcul des points pour le classement en tennis suisse selon la directive sur http://www.mytennis.ch
Un vrai casse-tête chinois pour tout le monde du tennis..
Merci
voilà je te l’ai envoyé par mail, mais après tout c’est tellement court que je peux aussi le mettre ici :
#include <iostream> #include <string> #include <stdlib.h> using namespace std; float rnd() { return (float) rand() / RAND_MAX;} class game { public: int score1,score2; bool simulate(float prob, int points=3) { score1=0; score2=0; while (true) { if (rnd()points && (score1-score2)>1) return true; if (score2>points && (score2-score1)>1) return false; } } }; class set { public: int score1,score2; int points1,points2; bool end(bool res) const { cout << score1 << "-" <<score2 <=6 || score2>=6){ if (score1==7 || score1-score2>1) return end(true); if (score2==7 || score2-score1>1) return end(false); } } } }; class match { public: int score1,score2; // sets int games1,games2; int points1,points2; bool simulate(float prob) { points1=0; points2=0; games1=0; games2=0; score1=0; score2=0; while (true) { set g; if (g.simulate(prob)) ++score1; else ++score2; points1+=g.points1; points2+=g.points2; games1+=g.score1; games2+=g.score2; if (score1==3){cout << "n"; return true;} if (score2==3){cout << "n"; return false;} } } }; int main(int argc, const char *argv[]) { srand(time(NULL)); for (float p=0.50; p<0.501; p=p+0.01) { match m; long points(0); long points1won(0); long games(0); long games1won(0); long sets(0); long sets1won(0); long lin1won(0); int matches1won(0); const int n=100; for (int i=0; i<n; ++i) { if (m.simulate(p)) ++matches1won; games+=m.games1+m.games2; games1won += m.games1; sets+=m.score1+m.score2; sets1won+=m.score1; points+=m.points1+m.points2; points1won+=m.points1; game g; if (g.simulate(p,48)) ++lin1won; } cout << p << " " <<(float)100*points1won/points << " " <<(float)100*games1won/games << " " <<(float)100*sets1won/sets << " " <<(float)100*matches1won/n << " " <<(float)100*lin1won/n << "n"; } return 0; }Moi j’aimerais bien le programme C++
Le comptage des points sur Swiss tennis est indéchiffrable. Je n’y comprends rien.
En gros si tu gagnes un match contre un R9 ou un R8 ou un R7 etc. te rapporte combien de bien, sachant que je suis R8 mais serai R7 en octobre prochain.
J’ai gagné un match contre un futur R6 4-6 5-0 et il a abandonné comment cela se passe ?
Si je perds des matchs contre des R9, R8 etc je perds combien de points ?
Merci beaucoup
ya pas de formule, c’est du calcul. Si quelqu’un veut le programme C++, je peux effectivement le rendre disponible…
Excellent j’adorerai avoir la formule mathématique.